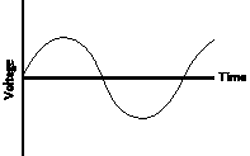
The sound produced by an instrument is a periodic or repeating change in air pressure. A microphone picking up that sound produces a signal which is usually a voltage whose waveform is directly analogous to the pressure wave as is shown in Figure 1. There are many advantages and disadvantages to using this method of representing sound, but one of the biggest problems is noise introduced by either the storage or transmitting media. In order to reduce this noise considerably, the analog representation of the signal can be replaced by a digital one. There are many ways to do this, but one of the most common is to use a method called Pulse Code Modulation or PCM, which is the system used in compact discs as well as DVD-Audio. How does one convert an analog signal into its PCM representation and what are the consequences?

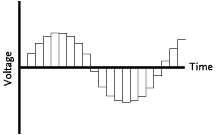When you sit and watch a movie, it looks like you’re watching movement on the screen. In fact, what you’re seeing is a number of still pictures in quick succession that fool your eyes into thinking that you’re seeing smooth movement. Digital audio works in basically the same way. In order to convert an analog signal into a digital equivalent, we need to sample (or measure) the voltage level at a regular rate called the sampling rate (equivalent to the frame rate in film). As is shown in Figure 2, the measurements are initially used to convert the smooth wave into a staircase representation. As is the case in film, we use this procedure to convert a continuous time to a discrete time signal. As a result, we lose the information between adjacent samples. In fact, it’s been proven that, in storing the sound in this manner, we don’t retain energy that has a frequency greater than half of the sampling rate. That is to say, in order to record frequencies up to 20,000 Hz, commonly accepted to be the highest pitch humans can hear, you’d need to record 40,000 samples per second. This is a very large number compared to the 24 frames per second seen in a typical film. In order to keep any unwanted high-frequency energy out of the system, the signal is first passed though a device known as an anti-aliasing filter which permits low frequencies to pass through but prevents those higher than one half of the sampling rate from reaching the sampling circuitry.

The next step in the procedure is to record the measurements as values that can be stored or transmitted. Unfortunately, it’s impossible to build a system able to make a perfect measurement of the voltage level -- just as it’s impossible to measure accurately a distance of 4.23 mm using a ruler that is marked in millimeters. 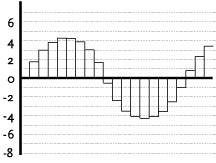As a result, we have to quantize or round off the measurement to the nearest value that the system can recognize. Comparing Figures 3 and 4, we can see that the quantization results in an intentional error in the measurements of the levels of the individual samples. The result of this quantization error is noise which, if not taken care of, can interfere with very quiet signals in the recording. The higher the number of quantization levels, the greater the accuracy of the measurements, thus lowering both the degree of possible error and the resulting system noise.

Once the quantization procedure is done, the individual samples are ready for storage. The attractive thing is that we can now simply list the consecutive levels of the samples as numbers. For example, looking at the quantized waveform in Figure 4, the levels of the samples are: 0, 2, 3, 4, 4, 4, 4, 3, 2, -1, -2, -4, -4, -4, -4, -4, -2, -1, 1, 2, 3.

This is essentially a digital representation of our original waveform.

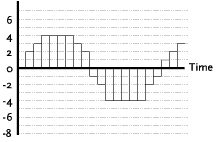
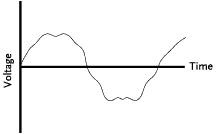
Rebuilding the analog signal from the stored digital signal begins by using a device that receives the string of stored numbers, and converts them into voltages, as is shown by the dotted line in Figure 5. 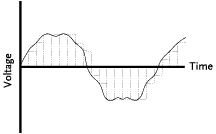By passing this staircase signal through another low-pass filter, the signal is smoothed (hence the typical name smoothing filter, although it’s also known as a reconstruction filter) and reconstructed into a waveform that closely resembles the original analog waveform, as is shown in Figure 6.

However, as can also be seen in Figure 6, the reproduction is not perfect. This is due to two reasons: firstly, the system does not have an infinite resolution in time. Secondly, the system does not have an infinite resolution in level. In order to improve the system, we have to increase the resolution in each dimension. Compact discs have a sampling rate of 44.1 kHz (therefore using 44,100 samples per second) and thus has a highest possible recorded frequency of 22,050 Hz. This value was set because most researchers agree that humans cannot hear frequencies above 20,000 Hz (this is a note a little more than 6 octaves above middle C). By comparison, DVD-Audio discs are capable of supporting sampling rates up to 96 kHz, resulting in recorded frequencies up to 48,000 Hz -- more than one octave above the maximum frequency recordable on a CD.

The DVD-Audio format also permits much higher resolution in the level measurement. CDs use what is known as a 16-bit system, meaning that the total number of possible quantized levels is 2 exponent 16 or 65,536 different levels (compare this with the total of 16 quantized levels in my example in Figure 4). DVD-Audios support a 24-bit system, using a total of 2 exponent 24 or 16,777,200 discrete levels.

In addition to these two improvements over the CD in the simple audio quality, DVD-Audio discs give the listener the option of having up to 6 channels of audio instead of CDs’ two. The result is a format that is technologically identical to the now-aging compact disc, with refinements that correct the limitations that were initially built into the original format.